2025.01.24＜高1・高2生必見！＞共通テストレビュー（数学編）
みなさんこんにちは！
ゴールフリー新田辺教室です。
1/18・1/19に共通テストが実施されました。
受験生の皆さんはお疲れ様でした。当教室の生徒も今は2次試験に向けて励んでいます。
さて、今年度は共通テストに様々な変化があったことをご存じでしょうか？
新科目：情報の追加が一番大きな変化でしたが、国語・数学・英語でもそれぞれ変化がありました。
来年・再来年に受験することを見据えてまずは形式を知っておきましょう。
数学①（数学ⅠＡ）の変更点
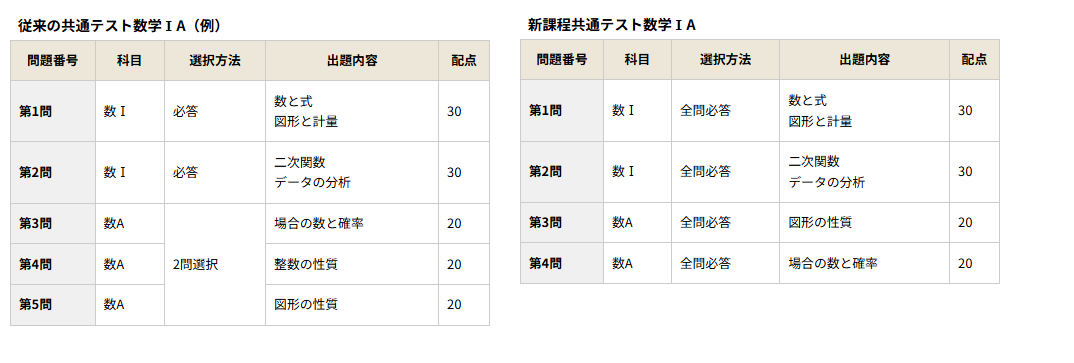上記が主な変化です。新課程で整数が削除された影響が出てきており、すべての問題が必答になりました。特に、整数は点数がとりやすい分野だったため平均点にも影響があるだろうと感じていました。（かくいう私も当時は確率が苦手だったため整数を解いていました。）数学②（数学ⅡＢ）の変更点
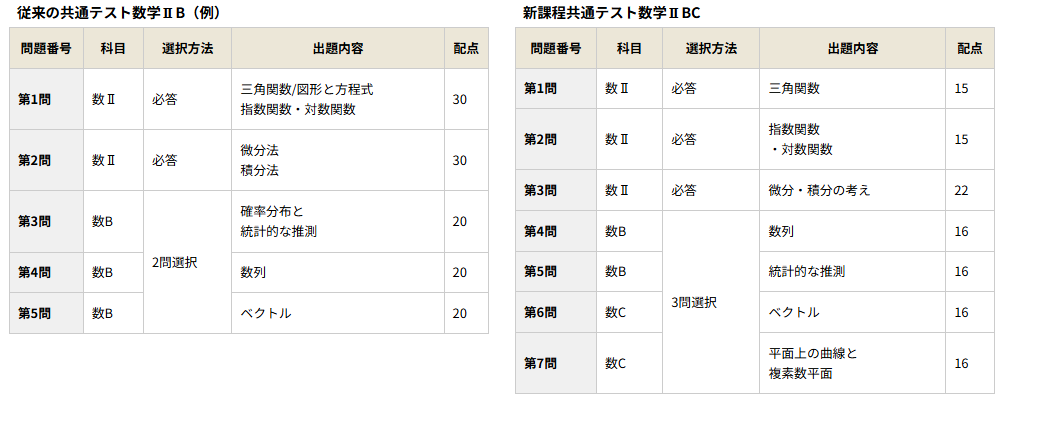
一番大きかったのは複素数平面の追加です。また大問構成が変わったことにより問題数もやや微増＋考えないといけない問題が増えるため10分伸びたにもかかわらず、時間が足りないということが懸念されました。また、点数配分が大きく変わったので、どこから解き始めるかなどの戦略が今まで以上に重要になりました。
では、以上の変更点を踏まえて今年度の試験を見ていきましょう。
問題はコチラからどうぞ
https://www.dnc.ac.jp/kyotsu/shiken_jouhou/r7/
数学①（数学ⅠＡ）レビュー
大問1 [1]数と式、集合と命題 （10点）[2]図形と計量（20点）
大問2 [1]2次関数（15点） [2]データの分析（15点）
大問3 図形の性質（20点）
大問4 場合の数と確率（20点）
平均点は56点台（昨年+5点）となっており、易化傾向が見られました。
共通テスト数学で絶対に守るべきことは2つです。
特に、2つ目は解き方に困ってしまう人には有効です。
例に出すと、
図形と計量→正弦定理・余弦定理
データの分析→分散、相関係数を求めさせる
図形の性質→チェバ・メネラウスの定理、方べきの定理
です。
今年度はチェバ・メネラウスの定理は使いませんでしたが、他は全て出題されています。前提を知っているだけで、それだけ悩むことは少なくなりますし、その分点数が取れます。
大問1
[1]方程式の解に関する問題でした。丁寧な誘導があり、きちんと従うことができれば、計算量・難易度どちらもそこまで高くないはず。
[2]平面上の2つの円に関し、円の中心、交点、共有する接線との接点を頂点とする三角形に関する問題でした。どれだけ作図を正確に書くことができるかと正弦定理・余弦定理をどの三角形で使うかをつかむことが高得点を取る秘訣です。
大問2
[1]公園の噴水を題材とした、放物線の式の決定や2次関数の性質を考察する問題でした。どのような条件で2次関数が決定されているかを正確に理解できれば満点を狙えます。
[2]都道府県別の外国人宿泊者数、日本人宿泊者数のデータに関する問題でした。分散と共分散の関係を聞かれており、どれだけ定義を理解できているかが点数に影響してきます。また、仮設検定はしっかりできるようになっておきましょう。
大問3
五面体の問題でした。同一平面上に4点があることがどのような図形的特徴を持つのかを理解しておく必要があります。
大問4
景品のあるゲームを行った場合に、主催者が妥当と判断するくじ引き料の設定について、期待値を計算し、判定する問題でした。序盤の確率を求める部分で間違ってしまい、点数が思うように取れなかった受験生が多かったと思います。あたり・はずれの事象がどうなっているかを逐一確認しましょう。
数学②（数学ⅡＢ）レビュー
大問1 三角関数（15点）
大問2 指数関数・対数関数（15点）
大問3 微積分法（22点）
大問4 数列（16点）
大問5 統計的な推測（16点）
大問6 ベクトル（16点）
大問7 複素数平面（16点）
平均点はこちらも56点台（昨年-1点）となっていました。時間がかつかつな中でどれなら自信をもって解けるかを判断して解かないといけません。選択問題は統計、ベクトルが比較的時間がかかりやすい分野（計算が複雑かつ多い）ではあるので数列＋複素数＋αがベターです。
大問1
三角関数の問題でした。Θの条件によってα,βがどのようなふるまいをするかを理解できれば、50％以上の点数はとれるはずです。最後もsinがcosに変わるとどうなるかという典型的な問題でした。
大問2
指数・対数の問題でした。主に対数方程式を正しく解くことができるかと常用対数表を用いて小数で表すことができるかが得点を取る鍵でした。初めの条件を間違えてしまうとすごく難しい問題に感じてしまうので、気を付けましょう。
大問3
導関数の等しい2つの3次関数の関係、面積との関連を調べる問題でした。序盤は3次関数のグラフの性質を解く問題であり、必ず正解したい。後半は、導関数の定積分が、元の関数とどのような関係があるかを理解していないと正解することは難しいです。
ここからが選択問題です。4問中3問を選ばなければいけません。
大問4
領域における格子点の個数を数列を用いて数え上げる問題でした。初めの直線に対応する格子点の個数は、Σの公式を知っていれば解けるはず。続く指数関数、値の決まっていない2次方程式もxが整数の時は必ず格子点上に点が取れることに気づくことができれば、難しいとは感じないはずです。
大問5
ある地域で栽培されたレモンのサイズ、重さに関するデータを題材とした問題でした。確率変数Ｚと正規分布の式が頭に入っていれば、キまでは正解したい。その後も数ⅠＡの仮設検定と同じ理論である。統計は覚えずらい代わりに問題の出題の仕方が大きく変わらないことが特徴です。公式を頭に叩き込みましょう。
大問6
座標空間における球面上の3点が正三角形をなす条件を考える問題でした。作図がしにくく、問題文を地道に追わないといけないため途中であきらめた人もいるかもしれません。シまでの難易度も計算量も高くないためここまではできるようになっておこう。シまでとれれば16点中12点です。
大問7
今年から入ってきた複素数です。2直線が垂直になる条件を考える問題でした。選択するならクまでは必ず全問正解しよう。ここまでは虚数のiの計算のみなので平面の知識はいりません。複素数平面の特徴として高校範囲では難しい問題を作りにくいというものがあるので、毛嫌いせず学習してほしいです。
以上、共通テスト数学の各大問レビューでした。
#個別指導塾#個別#塾#新田辺#京田辺#共通テスト#共テ#大学受験
ーーーーーーーーーーーーーーーーーーーーーーーーーー
ゴールフリー新田辺教室
〒610-0334
京都府京田辺市田辺中央１－４－３
STP新田辺北館
TEL☎：0774-65-1333
教室長：鉄川 諒汰（てつかわ りょうた）
